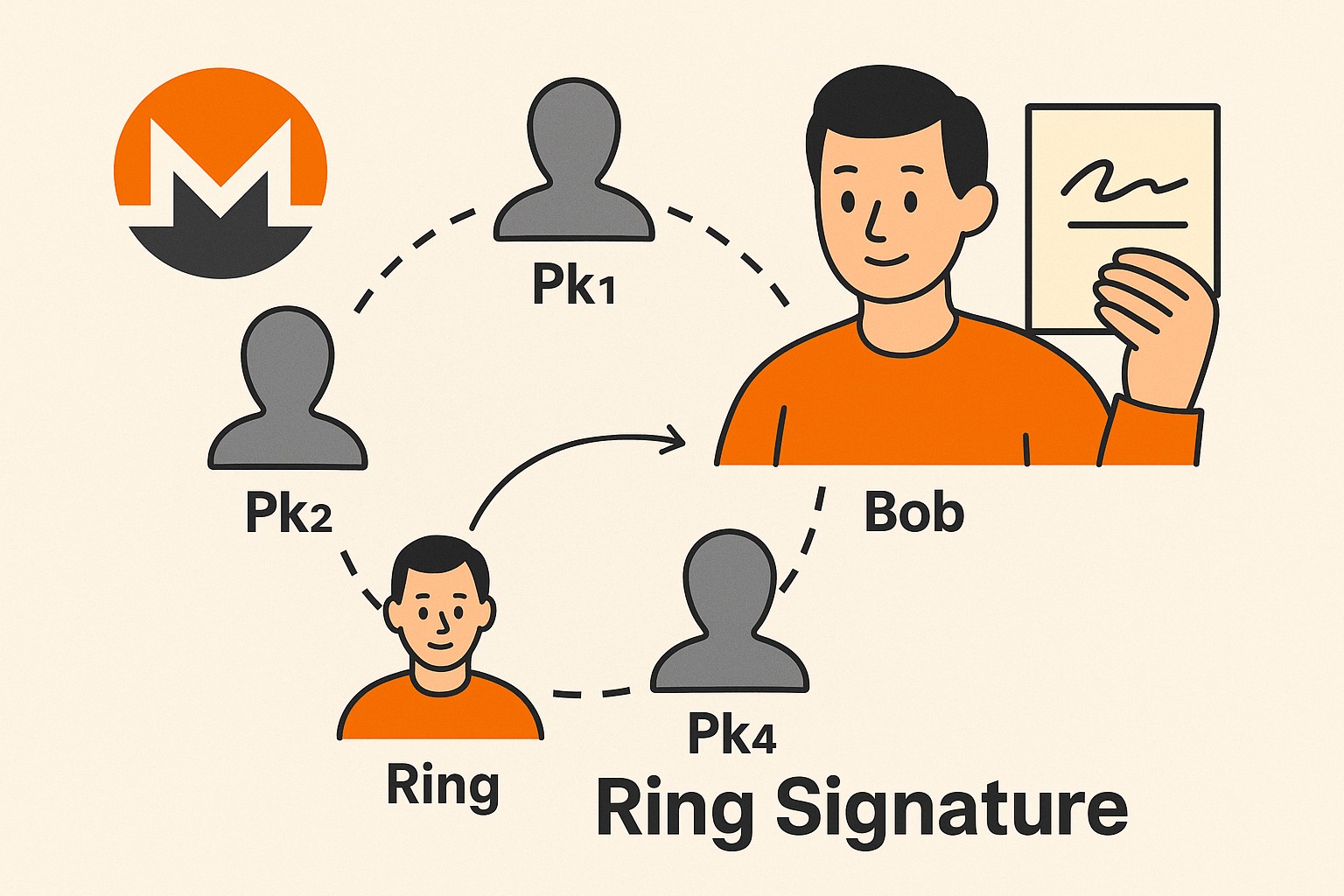
Introducció
- Monero és un tipus de criptomoneda, similar a Bitcoin. Es va llançar a l’abril de 2014 i, com moltes criptomonedes, està construït sobre la tecnologia blockchain. Això permet que Monero sigui descentralitzat, és a dir, que cap persona o organització en tingui el control exclusiu.
- Tant a Monero com a Bitcoin, tots els registres de transaccions s’emmagatzemen públicament a les seves respectives cadenes de blocs, fent-los visibles per a tothom. Aquesta transparència pot generar problemes de privadesa, ja que tercers poden utilitzar l’anàlisi de cadenes de blocs per rastrejar i vincular transaccions. Monero va ser dissenyat específicament per abordar aquests problemes de privadesa oferint un anonimat complet als seus usuaris.
- Monero està basat en el protocol CryptoNote, que va introduir funcions com ara adreces ocultes i signatures en anell per mantenir anònimes les identitats tant de l’emissor com del receptor. Avui ens centrarem en les signatures en anell i com funcionen a Monero.
Signatures d’Anell
Visió general
La idea principal darrere de les signatures en anell és que un usuari ![]() , que forma part d’un grup d’usuaris
, que forma part d’un grup d’usuaris
![]()
pot signar un missatge ![]() de manera que qualsevol que verifiqui la signatura estigui segur que un dels membres de
de manera que qualsevol que verifiqui la signatura estigui segur que un dels membres de ![]() va signar el missatge però no pugui saber de quin membre específic es tractava.
va signar el missatge però no pugui saber de quin membre específic es tractava.
Aquest protocol funciona sense la necessitat d’un tercer de confiança ni de la cooperació de tots els usuaris del grup. Cada participant només necessita un parell de claus privades i públiques. Per tant, qualsevol usuari pot triar els signants i generar la signatura de manera independent. Aquesta capacitat és especialment útil quan es difon informació de manera anònima, garantint alhora la integritat i l’origen del missatge.
Parelles de claus
Cada membre del grup té un parell de claus:
![]()
Quan un membre ![]() vol signar un missatge
vol signar un missatge ![]() , el procés de generació de signatures utilitza la clau privada
, el procés de generació de signatures utilitza la clau privada ![]() i les claus públiques dels altres membres
i les claus públiques dels altres membres ![]() . La signatura resultant es pot verificar sense revelar la identitat real del signant.
. La signatura resultant es pot verificar sense revelar la identitat real del signant.
L’exemple següent exposa amb més detall com es crea i verifica la signatura de l’anell:
Exemple: Bob Crea una Signatura d’Anell
Suposem que en Bob vol crear una signatura d’anell. Els seus passos són els següents:
- Calcula la clau del sistema
Calcula la clau del criptosistema aplicant el hash al missatge:![Rendered by QuickLaTeX.com \[k = h(m).\]](https://www.discrypt.cat/wp-content/ql-cache/quicklatex.com-7da3e0acaa89f2d9ecf79c67d529b257_l3.png)
- Determina el paràmetre
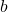
Trieu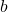 de manera que per a cada mòdul de clau pública
de manera que per a cada mòdul de clau pública 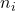 (amb
(amb 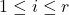 ) es compleixi que:
) es compleixi que:
![Rendered by QuickLaTeX.com \[2^b > n_i.\]](https://www.discrypt.cat/wp-content/ql-cache/quicklatex.com-4543dd8cea182977302d0a073759c821_l3.png)
(En RSA, una clau pública és
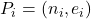 i una clau privada és
i una clau privada és  .)
.) - Genera valors aleatoris
- Genera un valor aleatori
 de
de 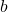 bits.
bits. - Per a cada clau pública del grup excepte la de Bob, genereu valors aleatoris de
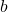 bits
bits 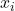 .
.
- Calcula els valors de
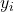
Per a cada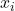 , calcula:
, calcula:
![Rendered by QuickLaTeX.com \[y_i = f_i(x_i).\]](https://www.discrypt.cat/wp-content/ql-cache/quicklatex.com-28d1864fdaeb07d6f83d53342f906a44_l3.png)
- Determina
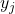 per a Bob
per a Bob
En Bob calcula el valor corresponent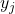 (on el seu parell de claus és
(on el seu parell de claus és 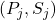 ) de manera que:
) de manera que:
![Rendered by QuickLaTeX.com \[C_{k,v}(y_1, y_2, \dots, y_r) = v.\]](https://www.discrypt.cat/wp-content/ql-cache/quicklatex.com-178368062f0081ad8c79f83196f7e8c7_l3.png)
C és una funció de combinació que aplica una XOR als valors i xifra els resultats amb la clau
, repetint-se fins que:
- Calcula
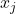
Per evitar exposar la seva clau privada, en Bob calcula:![Rendered by QuickLaTeX.com \[x_j = f_j^{-1}(y_j),\]](https://www.discrypt.cat/wp-content/ql-cache/quicklatex.com-eaef281e3e1ddbe28fc16503c2114075_l3.png)
utilitzant la seva clau privada
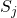 .
.
Signatura Final d’Anell
![]()
Procés de Verificació
- Per cada
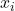 , calcula:
, calcula:
![Rendered by QuickLaTeX.com \[y_i = f_i(x_i).\]](https://www.discrypt.cat/wp-content/ql-cache/quicklatex.com-28d1864fdaeb07d6f83d53342f906a44_l3.png)
- Recalcula la clau del criptosistema:
![Rendered by QuickLaTeX.com \[k = h(m).\]](https://www.discrypt.cat/wp-content/ql-cache/quicklatex.com-7da3e0acaa89f2d9ecf79c67d529b257_l3.png)
- Comprova que
![Rendered by QuickLaTeX.com \[C_{k,v}(y_1, y_2, \dots, y_r) = v.\]](https://www.discrypt.cat/wp-content/ql-cache/quicklatex.com-178368062f0081ad8c79f83196f7e8c7_l3.png)
Signatures d’Anell en Transaccions Monero
Però, com ajuden exactament les signatures en anell a Monero a millorar la privadesa a l’hora de fer una transacció?
A Monero, quan un usuari envia una transacció, crea una signatura en anell utilitzant la seva clau privada i un conjunt de claus públiques d’altres usuaris no relacionats (anomenats “esquers”), seleccionats a partir de sortides anteriors de la cadena de blocs. Per a un observador extern, la transacció podria haver vingut de qualsevol membre de l’anell, fent que el remitent real sigui indistingible del grup.
Per a una mida d’anell de ![]() , hi ha
, hi ha ![]() possibles remitents a la cadena de blocs; només un és el que realment gasta, la resta són esquers. Això trenca el vincle entre les transaccions i el seu veritable origen, millorant significativament la privadesa.
possibles remitents a la cadena de blocs; només un és el que realment gasta, la resta són esquers. Això trenca el vincle entre les transaccions i el seu veritable origen, millorant significativament la privadesa.
Reflexions finals
- Tot i que les signatures en anell milloren molt la privadesa de Monero, no són perfectes. L’anàlisi estadística i de blockchain de vegades pot revelar l’aportació real entre els esquers, sobretot si els esquers no es trien de manera uniforme.
- L’efectivitat depèn de la mida del conjunt d’anonimat. Una mida d’anell de 2 (1 real + 1 esquer) és molt més feble que una mida d’anell de 10 o més.
- Monero imposa una mida mínima obligatòria d’anell (actualment 16) per garantir almenys 15 esquers per transacció.
- Monero també utilitza Ring Confidential Transactions (RingCT) per ocultar quantitats, combinant signatures d’anell amb compromisos de Pedersen perquè els valors de les transaccions romanguin confidencials i garanteixin que no es creïn ni es destrueixin monedes.
