
Bitcoin, i les criptomonedes en general, fan servir criptografia per garantir la possessió de
les monedes, entre molts altres aspectes. La seguretat es basa en problemes “difícils”
que garanteixen les propietats bàsiques, com la confidencialitat, la disponibilitat i la
integritat. Aquests tipus de problemes són coneguts com a funcions d’una sola direcció
(one-way) perquè són fàcils de calcular però increïblement difícil de desfer.
Un d’aquests problemes és el “problema del logaritme discret (DLP)”. No existeix cap
algoritme eficient capaç de resoldre aquest repte en el món “clàssic”, però les propietats
i capacitats dels ordinadors quàntics permeten la creació d’un nou conjunt d’algoritmes
capaços de solucionar aquests problemes.
Peter Shor va desenvolupar un algoritme capaç de desfer logaritmes discrets
eficientment. Si arribés a implementar-se, comprometria tots els sistemes informàtics
que depenen de la criptografia, un d’aquests, les criptomonedes.
No ens hem de preocupar massa, perquè la quantitat de potència de còmput necessari
per trencar les claus és major a la disponible actualment. Aquests tipus d’ordinadors són
extremadament sensibles a les pertorbacions, i a més, requereixen mecanismes per
mitigar els errors, entre ells trobem la implementació de redundància, fet que redueix
encara més l’eficiència.
Malgrat això, val la pena començar a pensar en el problema i intentar trobar la millor
situació abans que el Q-day arribi (el dia en el qual un ordinador quàntic sigui capaç de
trencar la criptografia).
Aquests ordinadors quàntics podrien ser capaços de trencar el DLP, donant com a
resultat el fet que algú podria computar la clau secreta associada a la clau pública,
permet-li gastar les monedes d’altres usuaris, conegut com un robatori. La principal
solució implica implementar qualsevol classe de criptografia post quàntica. Aquesta
criptografia “especial” té el superpoder de resistir els atacs dels ordinadors quàntics
perquè està basada en problemes “difícils”, fins i tot, per aquest tipus d’ordinadors.
Hi ha moltes maneres d’incloure algoritmes post quàntics en Bitcoin. Primer, podríem
implementar criptografia híbrida, és a dir, criptografia que combina les dues, tant la
clàssica com la post quàntica. Segon, podria ser implementat un esquema quàntic en
una fulla taproot, però continuar utilitzant la criptografia actual per tenir una salvaguarda.
Tercer, descartar l’algoritme i directament implementar un de post quàntic i ser usat com
l’actual. En aquest post ens centrarem en aquesta solució.
Hi ha una gran varietat d’algoritmes post quàntics, cadascun d’ells amb les seves
característiques. Generalment, els problemes “difícils” per als ordinadors quàntics
generen elements més grans, com ara claus o signatures, i són computacionalment
menys eficients. Això afecta el protocol Bitcoin de moltes maneres. La mida més gran de
les claus, per exemple, afectaran l’escalabilitat de la xarxa i a la quantitat de transaccions
per unitat de temps que podria processar la xarxa. El temps més gran de verificació no
només afectarà el rendiment, sinó que també influirà en la descentralització. Si es
necessita més potència per verificar les signatures, menys dispositius podran fer-ho,
reduint la quantitat de nodes i centralitzant, encara més, la cadena.
L’objectiu principal és trobar una solució que impliqui el mínim impacte per la xarxa; per
aconseguir-ho, l’algoritme post quàntic ha de tenir característiques similars als actuals.
Una particularitat de Bitcoin és la propietat de compatibilitat amb versions anteriors, és a
dir, que cada nova versió ha de funcionar perfectament amb versions anteriors. Això
comporta dificultats per incorporar canvis, per la qual cosa aquest nou algoritme hauria
d’implicar, també, el menor nombre de canvis possible.
Possibles solucions
Les solucions van des de la implementació de proves de coneixement nul (ZKP) fins a la
implementació d’un algoritme completament nou. Hi ha una gran varietat de criptografia
post quàntica cadascuna basada en diferents problemes “difícils” com ara: lattices, hash
functions, error correcting codes, multivariate polynomials or isogeny functions. Cada
tipus és útil en diferents situacions, per la qual cosa la nostra feina és trobar quin
s’adapta millor a Bitcoin.
Zero Knowledge Proof
La idea principal darrere la implementació de les ZKP a Bitcoin consisteix a ocultar la clau
pública de la xarxa però continuar podent verificar la signatura. D’aquesta manera,
podem continuar utilitzant la criptografia actual sense l’amenaça que ens robin les
monedes. El problema principal és que aquest tipus de prova requereix una gran quantitat
de dades, en alguns casos 50 KB, cosa que fa que sigui molt difícil incloure-la a Bitcoin. A
més, requereix una major potència computacional que ECDSA per verificar la prova, cosa
que limita el nombre de nodes capaços de executar aquesta tasca. La gran quantitat de
canvis necessaris per implementar-ho també genera dificultats que fan que sigui gairebé
impossible seleccionar aquesta solució.
Algoritmes post-quàntics
L’objectiu d’aquesta opció rau a implementar un esquema equivalent a l’ECDSA però
resistent als ordinadors quàntics. Hi ha moltes opcions diferents que garanteixen la
“resistència quàntica”, cadascuna té les seves pròpies mides de claus, cost
computacional i d’implementació. Després d’una anàlisi profunda, que no mostrarem
perquè ens portarà molt de temps, us mostrarem directament els resultats.
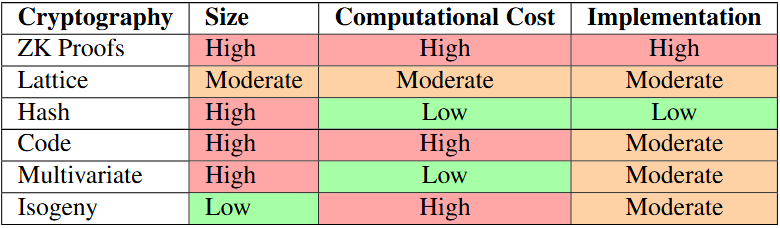
A la taula anterior hem comparat totes les solucions possibles, analitzant l’impacte de la
mida, el cost computacional i d’implementació. No busquem la millor opció en un cas,
com per exemple la mida més petita o el cost computacional més reduït, cada element és
igualment important. L’opció seleccionada haurà d’estar equilibrada, tot i que no ser la
millor en cap cas.
Un altre aspecte important és l’edat de l’algoritme, que és considerable per la seva
robustesa. Per demostrar que un algorisme no és segur, simplement s’ha de trobar una
falla o un problema. No obstant això, per demostrar que és segur, cada aspecte s’ha
d’analitzar amb precisió. L’edat és crítica per poder garantir aquesta seguretat, ja que, es
necessita temps per estudiar l’algoritme, per la qual cosa és molt més fiable un algorisme
que ha estat sotmès a una anàlisi profunda durant una dècada, que un altre que es va
presentar fa un o dos anys.
Conclusions
Tenint-ho tot en compte, la millor solució per al nostre cas és la criptografia basada en
lattices. Tot i que no és la millor opció en cap aspecte, en general, és la que compleix els
objectius. Proposem la implementació de FALCON-512 com a algorisme post quàntic de
clau pública. Té una mida de clau relativament petita, gairebé 1 KB, i un temps de
verificació inferior al d’ECDSA. Per poder utilitzar aquest algorisme, hauríem
d’implementar tot un grup nou d’opcodes, com gairebé qualsevol altre algorisme. Pel que
fa a la robustesa, s’ha presentat al projecte post quàntic del NIST, que ha estat estudiat i
analitzat en profunditat per desenes de grups diferents sense trobar cap problema
important, per la qual cosa sembla ser força segur.
Encara és massa aviat per suggerir una solució definitiva al problema. Tenint en compte
tot el que s’ha esmentat anteriorment i l’estudi que s’ha dut a terme al darrere, hem volgut
descartar les solucions menys viables per tal d’ajudar la futura investigació, de manera
que es pugui centrar en les opcions més prometedores.
Informació addicional
Com a material complementari, recomano molt l’article en què ens hem basat per
escriure aquest post. https://ddd.uab.cat/record/317512
