
Bitcoin and cryptocurrencies in general use cryptography to ensure the ownership of coins, among many other aspects. The security is based on “hard” problems that guarantee the basic properties, such as confidentiality, availability, and integrity. These problems are called one-way functions because they are easy to compute but incredibly difficult to undo them.
One of these problems is the “discrete logarithm problem (DLP)”. There does not exist any efficient algorithm to solve this challenge in the “classical” world, but the properties and capabilities of the quantum computers allow the creation of a new set of algorithms that resolve some of these problems.
Peter Shor developed an algorithm that can undo discrete logarithms efficiently. If this is implemented, it will compromise all the informatics systems that rely on cryptography, one of which will be cryptocurrencies.
We don’t have to worry about it because the amount of power needed to break the actual keys is larger than the available power nowadays. These kinds of computers are extremely sensitive to external disturbances, and they require mechanisms to mitigate errors, some of which are based on redundancy, reducing efficiency.
Despite this, it is worth starting to think about the concern now and try to come up with the best solution before Q-day arrives (the day when a quantum computer manages to break cryptography).
These quantum computers would be able to break the DLP, resulting in the fact that someone would compute the secret key associated with a public key, allowing them to spend other people’s coins, also known as theft. The main solution goes through implementing some sort of post-quantum cryptography. This “special” cryptography has the superpower to resist the quantum attacks by being based on “hard” problems, even though for these computers.
There are a lot of ways to include a post-quantum algorithm in Bitcoin. Firstly, we could implement hybrid cryptography combining both. Secondly, a quantum scheme could be implemented on a taproot leaf, but continue using the actual cryptography to have a backup. Thirdly, a new algorithm could be directly implemented and used as the actual ones. In this post, we will focus on the last option.
There exists a great variety of post-quantum algorithms, each one with its own characteristics. Generally, the “hard” problems for the quantum computers need bigger elements, such as keys or signatures, and are computationally less efficient. This affects the Bitcoin protocol in many ways. The larger keys, for example, will affect the scalability of the network and the transaction’s throughput. The slower verification time will not only impact the throughput but also influence the decentralization. If more power is needed to verify the signatures, fewer devices will be able to do it, reducing the quantity of nodes and centralizing the chain.
The main purpose is to find a solution that involves the least impact on the network; to achieve this, the post-quantum algorithm needs to have similar characteristics as the actual ones. One particularity of Bitcoin is the backwards compatibility property, meaning that every new version must work seamlessly with older versions. This leads to difficulties in incorporating changes, so this new algorithm should also involve the fewest changes.
Possible solutions
The solutions range from implementing zero-knowledge proofs to implementing a whole new algorithm. There are many types of post-quantum cryptography, based on different “hard” problems like lattices, hash functions, error correcting codes, multivariate polynomials, or isogeny functions. Each type is useful in different situations, so our job is to find which one fits better with Bitcoin.
Zero Knowledge Proofs
The main idea behind implementing ZKP on Bitcoin consists in hiding the public key from the network but still being able to verify the signature. By this way, we can continue using the actual cryptography without the threat of our coins being stolen. The main issue is that this type of proof requires a huge amount of data, in some cases 50 KB, making it so difficult to include on Bitcoin. Also, it demands a higher amount of computational power than ECDSA to verify the proof, limiting the number of capable nodes. The huge number of changes needed to implement this also generates difficulties, which makes it almost impossible to select this solution.
Post quantum Algorithms
The objective of this option lies in implementing a scheme equivalent to ECDSA but resistant to quantum computers. There are a lot, —like, a lot— of different options that ensure the “quantum resistance” quality. Each one has its own key sizes, computational and implementation costs. After a deep analysis, which we won’t show because it will take us ages, we will directly show you the results.
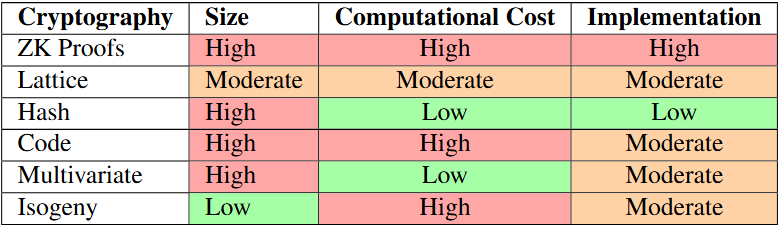
In the previous table, we compared every possible solution, analyzing the impact of the size, the computational and implementation cost. We are not looking for the best option in one case, for example, the smallest size or the lowest computational cost; each element is equally important. The selected option will have to be equilibrated, even though it is not the best in any case.
Another important aspect is the algorithm’s lifetime, which is important because of its robustness. To demonstrate that an algorithm is not secure, a flaw or an issue has to be found. Nevertheless, to prove that it is secure, each aspect must be analyzed accurately. Lifetime is critical because to be able to guarantee this security, you need time to study the algorithm, so it is much more reliable an algorithm that has been under a deep analysis for a decade, rather than other one that was presented one or two years ago.
Conclusions
Taking everything into account, the best solution for our case is lattice-based cryptography. Even though it is not the best option in any aspect, in general, it is the one that meets the objectives. We are proposing the implementation of FALCON-512 as a post-quantum resistance public key algorithm. It has a relatively small key size, almost 1 KB, and a lower verification time than ECDSA. To be capable of using this algorithm, we should implement a whole new group of opcodes, like almost every other algorithm. Referring to robustness, it has been submitted to the NIST post-quantum project, which has been studied and deeply analyzed by dozens of different groups without finding any big issues, so apparently, it seems to be quite secure. It is still too early to suggest a final solution for the problem. Considering everything mentioned above and the study that has been carried out behind, we wanted to discard the least viable solutions in order to help with future research so it could focus on the most promising options.
Further reading
For further reading I will highly recommend the article on which we have based on writing this post. https://ddd.uab.cat/record/317512
