NURWANTO Link Game Online x Ring Signatures in Monero

by Biel Castellarnau Ruiz

May 6, 2025

Blockchain Security, Cryptographic Primitives, Decoy Selection, Monero, Privacy & Anonimity, Research, Ring Signatures, RingCT

Introduction

Monero is a type of cryptocurrency, similar to Bitcoin. It was launched in April 2014 and, like many cryptocurrencies, is built on blockchain technology. This enables Monero to be decentralized, meaning no single person or organization has exclusive control over it.
In both Monero and Bitcoin, all transaction records are stored publicly on their respective blockchains, making them visible to anyone. This transparency can lead to privacy concerns, as third parties can use blockchain analysis to trace and link transactions. Monero was specifically designed to address these privacy issues by offering complete anonymity for its users.
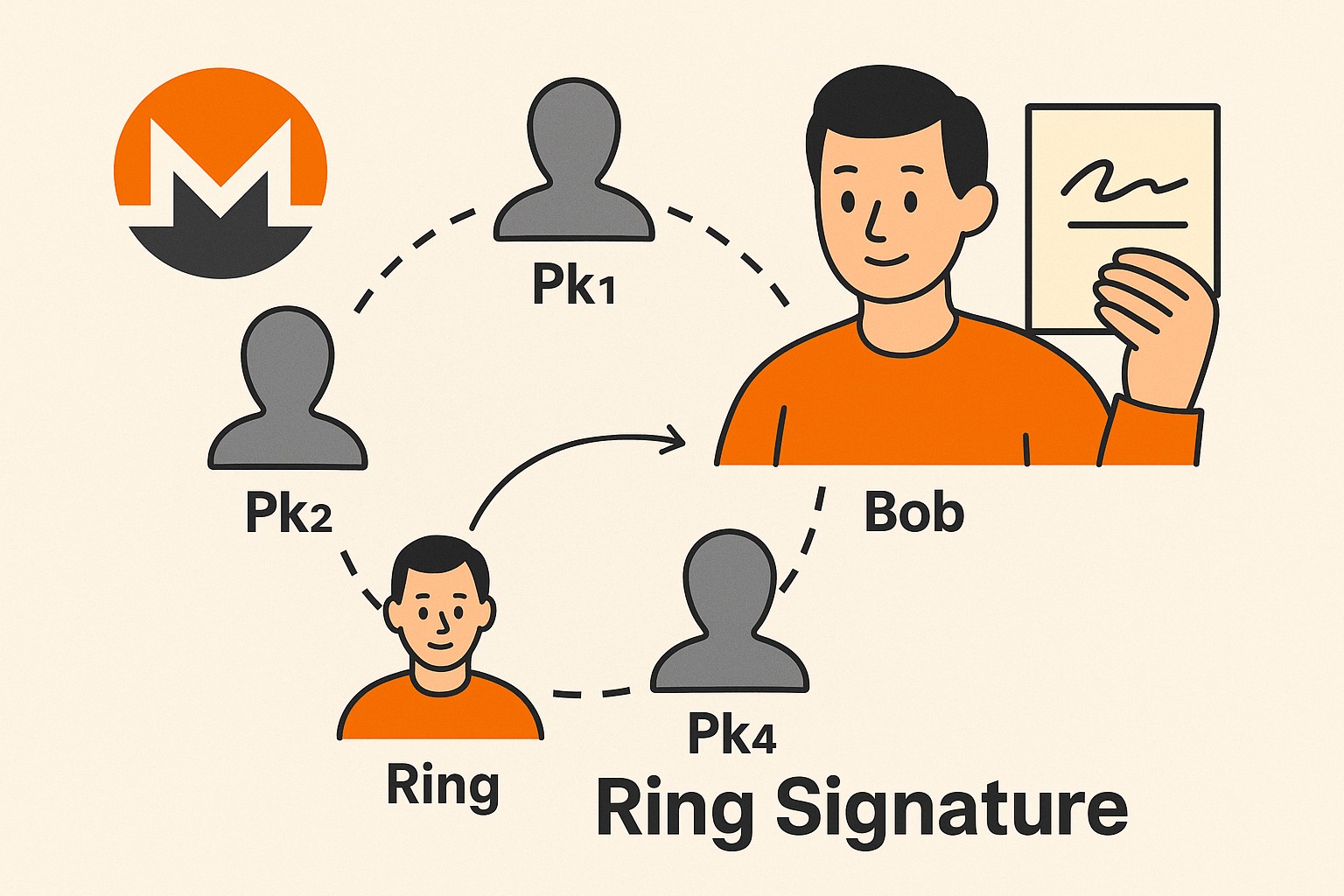
Monero is built on the CryptoNote protocol, which introduced features like stealth addresses and ring signatures to keep both the sender’s and receiver’s identities anonymous. Today, we’ll focus on ring signatures and how they function in Monero.

Ring Signatures

Overview

The main idea behind ring signatures is that a user $u$ , who is part of a user group

$R = {\,u_1,\,u_2,\,\dots,\,u_i},$

can sign a message $m$ such that anyone verifying the signature is assured that one of the members in $R$ signed the message but cannot know which specific member it was.

This protocol operates without the need for a trusted third party or the cooperation of all the users in the group. Each participant only needs a pair of private and public keys. Therefore, any user can choose the signers and generate the signature independently. This capability is especially useful when broadcasting information anonymously while still guaranteeing the integrity and origin of the message.

Key Pairs

Each group member holds a key pair:

${(P_1, S_1),\,(P_2, S_2),\,\dots,\,(P_i, S_i)}.$

When a member $j$ wishes to sign a message $m$ , the signature generation process utilizes the private key $S_j$ and the public keys of the other members ${P_1,\,\dots,\,P_{j-1},\,P_{j+1},\,\dots,\,P_i}$ . The resulting signature can be verified without disclosing the actual identity of the signer.

The following example exposes in more detail how the ring signature is created and verified:

Example: Bob Creating a Ring Signature

Suppose Bob wants to create a ring signature. His steps are as follows:

Calculate the System Key
Compute the key of the cryptosystem by hashing the message:
$k = h(m).$
Determine the Parameter $b$
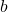
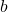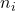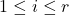Choose $b$ such that for every public key modulus $n_i$ (with $1 \le i \le r$ ) it holds that:
$2^b > n_i.$

(In RSA a public key is 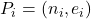$P_i=(n_i,e_i)$ and a private key is $S_i=(n_i,d_i)$ .)
Generate Random Values

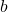Generate a random value $v$ of $b$ bits.
For each public key in the group except Bob’s, generate random 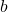$b$ -bit values $x_i$ .

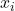Compute 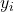$y_i$ Values
For each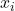 $x_i$ , compute:
$y_i = f_i(x_i).$
Determine 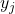$y_j$ for Bob
Bob calculates his corresponding value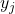 $y_j$ (where his key pair is 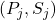$(P_j,S_j)$ ) so that:
$C_{k,v}(y_1, y_2, \dots, y_r) = v.$

C is a combination function that XORs values and encrypts the results with the key $k$ , repeating until:

$C_{k,v}(y_1,\dots,y_i)= E_k\bigl(y_i \oplus E_k(y_{i-1} \oplus \dots \oplus E_k(y_1 \oplus v))\bigr).$

Compute $x_j$
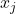
To avoid exposing his private key, Bob computes:
$x_j = f_j^{-1}(y_j),$

using his private key $S_j$ .

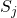Final Ring Signature

$\omega = {P_1,\,P_2,\,\dots,\,P_i,\;v,\;x_1,\,x_2,\,\dots,\,x_i}.$

Verification Process

For each 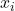$x_i$ , compute:
$y_i = f_i(x_i).$
Recompute the cryptosystem key:
$k = h(m).$
Check that
$C_{k,v}(y_1, y_2, \dots, y_r) = v.$

Ring Signatures in Monero Transactions

But how exactly do ring signatures help Monero improve privacy when making a transaction?

In Monero, when a user sends a transaction, they create a ring signature using their private key and a set of public keys from other unrelated users (called “decoys”), selected from previous blockchain outputs. To an outside observer, the transaction could have come from any member of the ring, making the real sender indistinguishable from the group.

For a ring size of $n$ , there are $n$ potential senders on the blockchain; only one is the actual spender, the rest are decoys. This breaks the link between transactions and their true origin, significantly enhancing privacy.

Final Thoughts

While ring signatures greatly improve Monero’s privacy, they’re not perfect. Statistical and blockchain analysis can sometimes reveal the real input among decoys, especially if decoys aren’t uniformly chosen.
The effectiveness depends on the anonymity set size. A ring size of 2 (1 real + 1 decoy) is far weaker than a ring size of 10 or more.
Monero enforces a mandatory minimum ring size (currently 16) to ensure at least 15 decoys per transaction.
Monero also uses Ring Confidential Transactions (RingCT) to hide amounts, combining ring signatures with Pedersen commitments so that transaction values remain confidential while ensuring no coins are created or destroyed.

Monero Whitepaper

NURWANTO Link Game Online x Ring Signatures in Monero – DISCRYPT

NURWANTO membongkar hubungan link game online dengan Ring Signatures di Monero dari sudut yang lebih tajam, bukan sekadar istilah yang lewat begitu saja. Fokusnya ada pada jejak, pola baca, dan cara memahami konteksnya tanpa kehilangan arah.

Di sisi lain, pembahasan DISCRYPT membantu merapikan konsep Monero agar lebih mudah dicerna, terutama saat istilah teknis terlihat rumit. Dari sini, pembaca bisa melihat bagaimana kata kunci di judul saling terhubung dan membentuk satu tema yang utuh.

Kalau Anda ingin menangkap benang merah antara link game online, Ring Signatures, dan Monero, halaman NURWANTO ini memberi titik masuk yang lebih jelas. Baca pelan-pelan, lalu bandingkan sendiri sudut pandangnya.

Ring Signatures in Monero